En el mundo de los datos y los programas informáticos, el concepto de Machine Learning puede parecer un hueso duro de roer, lleno de matemáticas complicadas e ideas complejas. Por eso hoy quiero ir más despacio y revisar los conceptos básicos que hacen que todo esto funcione. Voy a empezar una nueva serie de artículos que voy a llamar MLBasics.
Vamos a revisar una serie de conceptos sencillos: los modelos que son el ABC de la ML. Piensa en ello como empezar con las piezas fáciles de un gran rompecabezas. Vamos a volver a las cosas sencillas, donde es fácil entender lo que está pasando.
Así que acompáñanos mientras lo desglosamos y lo aclaramos todo.
Sumerjámonos en la Regresión Lineal Simple, paso a paso, ¡juntos! 👇🏻🤓
Tabla de contenidos
1. Introducción a la regresión lineal simple
El ámbito del análisis predictivo es muy amplio, pero en su núcleo se encuentra la Regresión Lineal, el método más sencillo para dar sentido a las tendencias de los datos.
Mientras que sus extensiones en múltiples variables pueden parecer desalentadoras, nuestro enfoque de hoy se reduce a la Regresión Lineal Simple.
¿El objetivo principal? Encontrar una relación lineal entre:
- La variable independiente o predictor.
- La variable dependiente o salida.
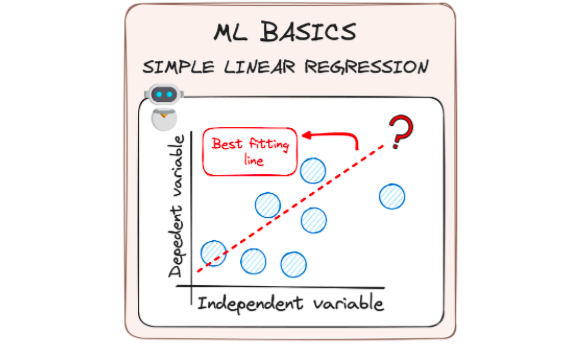
En lenguaje llano, la Regresión Lineal consiste en encontrar una línea recta que muestre cómo dos cosas están conectadas – como cuánto estudias (esa es la parte independiente) y tus resultados en los exámenes (esa es la parte dependiente).
La idea es ver cómo una cosa puede predecir la otra.
Suena interesante, ¿verdad?
Pues ahora… vamos a intentar encontrarle algún sentido a la Regresión Lineal preguntándonos…
2. ¿Cómo calcularlo matemáticamente?
Piénsalo como un trabajo en equipo en el que dos cosas trabajan juntas:
- Una que depende de otra: el resultado.
- Otra que es independiente, la llamaremos predictor.
Tienen que tener una relación en línea recta, algo así como seguir un camino recto en un mapa que nos lleve a las respuestas que buscamos.
Ahora bien, encontrar el camino perfecto -o, en nuestro caso, la línea de mejor ajuste- no consiste en hacer conjeturas.
Cuando hablamos de datos numéricos, utilizamos una fórmula única para identificar la línea óptima en Regresión Lineal. Entendiendo que existe una correlación lineal entre las variables, podemos aplicar directamente una función lineal para determinar nuestro predictor.
En esta pequeña receta matemática, hay 4 variables principales:
- Y es nuestro resultado.
- B establece dónde empieza la recta.
- A es el ángulo de nuestra pendiente.
- X es nuestro predictor.
Usando esto, podemos dibujar una línea recta a través de nuestros puntos de datos que nos muestran la conexión entre las dos variables que estamos viendo.
Ahora que sabemos cómo definir una relación de este tipo, puede que te preguntes…
3. ¿Cómo definir este mejor ajuste?
La idea final es bastante clara: queremos una línea que no cometa muchos errores.
¿Y qué consideramos un error?
Un error, en este caso, significa lo lejos que está nuestra suposición de lo que realmente ocurre. Así que definiremos un error como la diferencia entre nuestro valor predicho y el real.
Error de formulación matemática.
Por lo tanto, la mejor línea es la que tiene los menores errores. O dicho de forma sencilla…
Las pequeñas diferencias entre lo que pensamos que ocurriría (nuestra predicción) y lo que realmente ocurrió (el valor real).
Tenemos un nombre especial para estos errores: los llamamos residuales. Queremos que esos residuos, o errores, sean lo más pequeños posible para que nuestras predicciones sean superprecisas.
Imagen del autor. Representación de los residuos
Y esto nos lleva a la siguiente pregunta natural…
4. ¿Cómo obtener matemáticamente esta recta de mejor ajuste?
Si recordamos la ecuación lineal, tenemos dos variables importantes, que tenemos que averiguar y que llamaremos pesos a partir de ahora:
- A que representa el ángulo de nuestra pendiente.
- B que define dónde empieza la recta.
Para ello, utilizamos una herramienta especial llamada función de coste. Piensa en la función de coste como un método que nos ayuda a encontrar los valores óptimos para nuestras ponderaciones.
Para la regresión lineal, utilizamos como función de coste el Error Cuadrático Medio (ECM), una métrica que captura la desviación cuadrática media entre los valores predichos y los resultados reales.
Al elevar al cuadrado cada error antes de calcular la media, nos aseguramos de que todas las discrepancias, independientemente de su dirección -positiva o negativa-, contribuyan por igual a la medida global.
Este proceso acentúa los errores más grandes, proporcionando una imagen clara del rendimiento del modelo.
Formulación matemática errónea.
Una vez que tenemos nuestra función de coste, hay dos formas principales de evaluar un problema de optimización de este tipo:
4.1 Mínimos cuadrados ordinarios u OLS
El objetivo de los mínimos cuadrados ordinarios (MCO) es determinar los coeficientes óptimos A y B minimizando la suma de los errores de predicción al cuadrado.
Aprovechando el cálculo, explotamos las propiedades de las derivadas parciales para localizar los mínimos de la función de coste, donde estas derivadas son iguales a cero.
Resolviendo esos problemas matemáticos, obtenemos una fórmula matemática cerrada exacta tanto para A como para B, lo que nos proporciona una ruta directa hacia el modelo lineal más preciso.
Imagen del autor. Obtención de funciones matemáticas cerradas OLS.
4.2 Descenso gradual
El descenso gradual es un algoritmo de optimización fundamental que se utiliza para minimizar la función de coste, ayudándonos a encontrar los valores de peso más precisos para nuestro modelo predictivo.
Imagínate que te encuentras en lo alto de una colina y que tu objetivo es el valle que hay debajo: éste representa el punto mínimo de nuestra función de coste.
Para alcanzarlo, empezamos con unas conjeturas iniciales para nuestros pesos, A y B, e iterativamente refinamos estas conjeturas.
El proceso es similar al descenso de una colina: a cada paso, evaluamos nuestro entorno y ajustamos nuestra trayectoria para asegurarnos de que cada paso siguiente nos acerque al fondo del valle.
Estos pasos están guiados por la tasa de aprendizaje, un hiperparámetro vital simbolizado como lr en las ecuaciones. Esta tasa de aprendizaje controla el tamaño de nuestros pasos o los ajustes de los parámetros A y B, garantizando que no sobrepasemos el mínimo.
Ecuaciones iterativas ponderadas. Cada paso nos acerca más a la solución óptima.
A medida que damos cada paso, calculamos las derivadas parciales de la función de coste con respecto a A y B, denotadas como dA y dB respectivamente. Estas derivadas nos señalan la dirección en la que la función de coste disminuye más rápidamente, algo así como encontrar la pendiente más pronunciada en nuestra metafórica colina.
Las ecuaciones actualizadas para A y B en cada iteración, teniendo en cuenta la tasa de aprendizaje, son las siguientes:
Este meticuloso proceso se repite hasta que llegamos a un punto en el que la disminución de la función de coste es insignificante, lo que sugiere que hemos llegado o estamos cerca del mínimo global, nuestro destino donde se minimiza el error de predicción y se maximiza la precisión de nuestro modelo.
Imagen del autor. Representación del descenso gradual.
5. Evaluación
Muy bien, vamos a hablar de cómo comprobar si nuestro modelo de regresión lineal simple está haciendo un buen trabajo. Hay dos formas principales de hacerlo:
5.1 Coeficiente de Determinación o R-Cuadrado (R²):
Esta es una forma elegante de decir qué parte de los cambios en lo que estamos tratando de predecir puede ser explicado por nuestra variable independiente – la que creemos que está causando el cambio.
Es como una puntuación entre 0 y 1. Si se aproxima a 1, el resultado es positivo.
- Si se acerca a 1, significa que nuestro modelo explica gran parte de lo que ocurre.
- Si está más cerca de 0, no tanto.
5. 2 Error cuadrático medio (RMSE):
Se refiere a la cantidad de error que hay en nuestras predicciones. Es como tomar todos nuestros errores, elevarlos al cuadrado (lo que los hace todos positivos), promediarlos y luego tomar la raíz cuadrada de ese promedio. Así obtenemos un número que nos indica, por término medio, lo alejadas que están nuestras predicciones.
Cuanto menor sea este número, mejor será la predicción de nuestro modelo.
6. Supuestos para aplicar la regresión lineal
Para que la regresión lineal funcione bien, hay algunas cosas clave que debemos tener en cuenta antes de aplicarla a un conjunto de datos aleatorios:
6.1 Linealidad de las variables
Ambas variables, independiente y dependiente, tienen que estar conectadas de forma lineal. Esto significa que si una de ellas sube o baja, la otra tiende a seguir un patrón lineal predecible.
6.2 Independencia de los residuos
Respecto a los errores: son los pequeños errores que cometemos al predecir cosas. Queremos asegurarnos de que estos errores no siguen ningún patrón ni dependen unos de otros. Deberían producirse de forma aleatoria.
6.3 Distribución normal de los residuos
Además, cuando observamos la media de todos estos errores (o residuos, como se denominan), deben distribuirse de forma normal, como si la mayoría de ellos se agruparan en torno al centro (que debe estar próximo a cero).
6.4 La misma varianza de los residuos
Por último, estos errores deben permanecer constantes en su dispersión, es decir, no deben aumentar o disminuir a medida que nos movemos por los datos. Deben variar, pero la cantidad de variación debe ser la misma en todo momento.
Conclusión
En nuestro viaje MLBasics, hemos comenzado a desmitificar la Regresión Lineal Simple, mostrando su papel fundamental en la comprensión de las tendencias de datos.
Hemos explorado la relación entre las variables independientes y dependientes, haciendo hincapié en la minimización de errores para obtener predicciones precisas.
Nuestro debate ha incluido enfoques matemáticos como los mínimos cuadrados ordinarios (MCO) y el descenso gradiente para optimizar el modelo.
Evaluamos la eficacia del modelo utilizando las métricas R² y RMSE y subrayamos la importancia de cumplir los supuestos clave para una aplicación satisfactoria.
Permanece atento a nuestro próximo artículo, en el que llevaremos la teoría a la práctica en un proyecto integral, demostrando la Regresión Lineal Simple.
Puedes suscribirte a mi newsletter DataBites para estar al día y recibir mis contenidos. ¡Prometo que será único!
También puedes encontrarme en Twitter y LinkedIn.